Experiment 6 Capacitance and time constant

Experiment 6
Topic: Capacitors
Title: Capacitance and time constant
Objective: To determine the capacitance of capacitors and the time constant of an R-C circuit.
Theory:

The R-C circuit

When the switch is closed, charging takes place. The charge stored Qo in a fully capacitor is given by

When the switch is open, the capacitor will discharge through the resistor. The relationship of voltage can now be given as

,

where 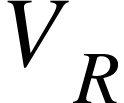and 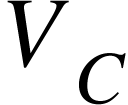are the potential differences across the resistor and the capacitor respectively. Hence

Since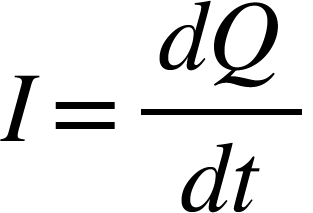 therefore

Solving for Q(t) and I(t) using

Apparatus:
(i) A 6 V d.c. power supply
(ii) An switch
(iii) A d.c. milliammeter
(iv) A stopwatch

used stopwatch lap to mark the time

(v) Resistor-pack

two types of resistor pack
used either

(vi) Two connecting wires with a crocodile clip at one end
(vii) Some connecting wires
(viii) A capacitor labelled C

Procedure:

Caution: Before start the experiment, the capacitor has to be fully discharged. This is done by short-circuiting its terminals. Check the capacitor, the time to discharge should be no more than 3 minute when attached to 6600Ω.

(a) The circuit was set-up with switch S as shown in Figure 7. X and Y are crocodile clips meant for connection to the resistor-pack for selections of R, where R is the effective resistance across X and Y.

Figure 7.

The assembly of the experiment

(b) Started with R = 6600 Ω, switch S was closed, and R was decreased in stages by proper selection of combination of resistors from the resistor-pack until the reading of current I_o in the milliammeter was about 1.0 mA[1].
The value of I_o and the corresponding resistance R_o was recorded.

(c) Switch S is opened and short-circuit the terminals of the capacitor with a short connecting wire to fully discharge it.
(d) Switch S is closed again to charge the capacitor until the reading of the milliammeter shown Io once again.
(e) Then switch S is opened and simultaneously started the stopwatch, and the reading of the milliammeter was observed.

The stopwatch is stopped when the current reached a certain value of I[2]. 

 this action could not be done. what should be done is, while the current is decreasing at certain amount (that have been manipulate before the switch is opened) this could be done smoothly by using the stopwatch  Lap.

The time t and the corresponding value of I of the milliammeter was recorded.

(f) The steps (d) and (e) was repeated to obtain a new set of I and t. All the readings was recorded and tabulated
(g) Graph of against t was plotted and its gradient k was determined.
(h) The time constants for the R-C circuit was determined.
(i) The capacitance C was calculated.
(j) From the graph of against t, an expression was deduced for current I as a function of time t. 

Reading

current, I	times			I0 /I
	t1	t2	average

---

[1] Reducing the resistance,R from resistor pack will give higher current if the current is low.
[2] Its mean that the maximum current will reduce (when capacitor discharge) in a certain time. So technically the reduced current need to be set at certain value to take its time to reduce, example: maximum current is 1 mA, the current is set for 0.9 mA, record the time taken to reduce to 0.9 mA, this is the first set of data. Then charged the capacitor so that current is maximum again, then set the current for 0.8 mA, record the time taken to reduce to 0.8 mA.